run

SABL
Summary
Move post-processing to CPU to avoid memory limitations
Prediction - in sample
Prediction - out of sample

clear all; close all;
global C P M Cpar E

SABL

%   Results directory

    outpath = 'SABL_results/Specification3/beta_0 = p3,att4cert/beta_1 = c/beta_2 = posterior,wtp/beta_3 = quality/beta_4 = c,hiimpuls,hiconscien/beta_5 = topics,himarketexper,hiprodknow,age40over,gender,hifinlit,hinum/price zero-mean adjusted, all individual characteristics +1-1 coded, multiplicative sigma, fixed s = 0.75';

%   Enable GPUs

    P.useGpu = true;

%   Topics
    P.topic = {'Sup','Div','Fee','Deb'};

%   Choose specification - default is Specification 1

    P.specification3 = true;
    P.forceRational  = false;
    P.forceFryer     = false;
    P.fixedS         = 0.75;

%   Import CSV data

    if (P.specification3)
       [spec2.responseid,...
        spec2.topic1,...
        spec2.choice1,...
        spec2.att5goodbad1,...
        spec2.topic2,...
        spec2.choice2,...
        spec2.att5goodbad2,...
        spec2.topic3,...
        spec2.choice3,...
        spec2.att5goodbad3,...
        spec2.topic4,...
        spec2.choice4,...
        spec2.att5goodbad4,...
        spec2.hardeasyseq,...
        spec2.choice_pay2,...
        spec2.att2gender,...
        spec2.att3age,...
        spec2.att4cert,...
        spec2.goodbadseq,...
        spec2.price,...
        spec2.topic_seq,...
        spec2.age,...
        spec2.gender,...
        spec2.p3,...
        spec2.IMC1,...
        spec2.IMC2,...
        spec2.hifinlit,...
        spec2.hinum,...
        spec2.hiprodknow,...
        spec2.hiconscien,...
        spec2.hiimpuls,...
        spec2.hismartpast,...
        spec2.hifinmetrisktol,...
        spec2.himarketexper,...
        spec2.age40over,...
        spec2.choice_pay1] = ...
        u_importCSV('supervideo2_data_prepared_fryer_spec2.csv');
    end

%   Choose a model

    model1s2 = true;

%   Hold out rows from the estimation for making predictions later

%     P.dataRowsHeldOut = [];

    sdOriginal = rng;
    rng(168,'twister');
    dataRowsPermute = randperm(length(spec2.price));
    P.dataRowsHeldOut = dataRowsPermute(1:100);
    rng(sdOriginal);

    % P.dataRowsHeldOut = 1:1:800;
    % P.dataRowsHeldOut = 801:1:1600;
    % P.dataRowsHeldOut = 1601:1:2400;
    % P.dataRowsHeldOut = 2401:1:3200;
    % P.dataRowsHeldOut = 3201:1:length(m.data.choose_wtp);   % Rows to leave out during model estimation

    P.dataRowsInEstimation = 1:length(spec2.choice_pay2);

    P.dataRowsInEstimation(P.dataRowsHeldOut) = [];

%   Adjustments

    u_adjustdata(P.dataRowsInEstimation,spec2);

    adjustPosNeg = @(x) 2.*x - 1;
    adjustPrice  = @(x) (x-mean(x))./100;
    isVal = @(x,y) all(x == y(ones(length(x),1),:),2);
    adjustP3 = @(x) 2.*(x-1)-1;
    adjustGender = @(x) 2.*(x-1)-1;

%   Define clarity classes

    P.d_Quality = permute((cell2mat(spec2.goodbadseq(P.dataRowsInEstimation)) == 'G'),[1 3 2]);
    P.d_Quality_R = 1 - P.d_Quality;

    P.d_ClarityT(1,1,1,1,1,:,1,1) = [1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0];  % Super consolidation
    P.d_ClarityT(1,1,1,1,1,:,1,2) = [1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 0];  % Diversification
    P.d_ClarityT(1,1,1,1,1,:,1,3) = [1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0];  % Fees
    P.d_ClarityT(1,1,1,1,1,:,1,4) = [1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0];  % Debt consolidation

% Transform the classification into a time series for each individual

    localDataChoiceSetTopic = reshape([P.x23 P.x24 P.x25 P.x26 ...
                                       P.x27 P.x28 P.x29 P.x30 ...
                                       P.x31 P.x32 P.x33 P.x34 ...
                                       P.x35 P.x36 P.x37 P.x38],...
                                       size(P.d_Quality_R,1),...
                                       size(P.d_Quality_R,3),...
                                       length(P.topic));
    localDataChoiceSetTopic = permute(localDataChoiceSetTopic,[1 4 2 5 6 7 8 3]);  % 4,5,6,7,8 were singleton
    P.d_Clarity = sum(bsxfun(@times,localDataChoiceSetTopic,P.d_ClarityT),8);

% Calculate update sequences

    P.updateRational = bsxfun(@times,P.d_Clarity,(2.*P.d_Quality - 1));
    P.updateRational_R = bsxfun(@times,P.d_Clarity,(2.*P.d_Quality_R - 1));   % Left-side and right-side are the same clarity class

    P.d_Quality = adjustPosNeg(P.d_Quality);
    P.d_Quality_R = adjustPosNeg(P.d_Quality_R);
    if P.useGpu
        P.d_Quality = gpuArray(P.d_Quality);
        P.d_Quality_R = gpuArray(P.d_Quality_R);
        P.d_Clarity = gpuArray(P.d_Clarity);
        P.updateRational = gpuArray(P.updateRational);
        P.updateRational_R = gpuArray(P.updateRational_R);
    end

%   Define rationality class

    P.rationality = {'Rational','Fryer'};

%   Set up a model

    if model1s2

        P.dataColumnsLambda      = [3 13 6];
        P.thetaColumnsLambda     = [1  2 3];
        P.IndicatorLambda0       = [1 -1 0];
        P.IndicatorLambda0_R     = [1  1 0];
        P.IndicatorS             = [0  0 1];

        P.dataColumnsChoiceSequence = [19 20 21 22];

        P.dataColumnsOutcome_R = 1;
        P.dataColumnsOutcome = 2;

%       P.dataColumnsWtp = [18 4  5  7  8  9 10 13 39 40 6];
%       P.IndicatorWtp   = [ 1 1  1  1  1  1  1 -1  1  1 1];
%       P.IndicatorWtp_R = [ 1 1  1  1  1  1  1  1  1  1 1];
        P.dataColumnsWtp = [18];
        P.IndicatorWtp   = [ 1];
        P.IndicatorWtp_R = [ 1];

%       P.thetaColumnsWtp =    [ 6 7 8 9 10 11 12 13 14 15 16];
%       P.thetaColumnsPosterior = 17;
        P.thetaColumnsWtp =    [4];
        P.thetaColumnsPosterior = 5;

%       P.dataColumnsChoiceSetXAdvisor = [11 12 13];
%       P.dataColumnsChoiceSetXIndiv = [4 5 7 8 9 10];
        P.dataColumnsChoiceSetTopic = 23:1:38;

        % P.thetaColumnsInteractionXAdvisorXIndiv = [18 19 20 21 22 23 24 25 26 27 28 29];
        % P.thetaColumnsInteractionXIndivTopic = 20:1:43;
        % P.thetaColumnsInteractionQualityRXIndiv = [20 21 22 23 24 25];
        % P.thetaColumnsInteractionQualityRTopic = [26 27 28 29];

        P.thetaColumnsQualityR = 6;

        % P.thetaColumnsChoiceSetXAdvisor = [31 32 33];
        % P.thetaColumnsChoiceSetTopic = [34 35 36 37];
        % P.thetaColumnsChoiceSetConstant = 34;

        P.thetaColumnsSigma = 7;

        % P.fixedSigma = 0.01;
        % if P.useGpu
        %     P.fixedSigma = gpuArray(P.fixedSigma);
        % end

        %
        % Rationality class logit
        %
        % P.dataColumnsRationalityXIndiv  = [ 4  5  7  8  9 10 39 40 6];
        % P.thetaColumnsRationalityXIndiv = [24 25 26 27 28 29 30 31 32];
        P.dataColumnsRationalityXIndiv  = [39 40 6];
        P.thetaColumnsRationalityXIndiv = [8  9 10];

        %
        % Clarity class logit
        %
        P.dataColumnsClarityXIndiv      = [ 4  5  7  8  9 10];
        P.thetaColumnsClarityXIndiv     = [11 12 13 14 15 16];
        P.thetaColumnsClarityC          = [17 18 19 20];

        %
        % Number of parameters
        %
        tableSize = 20;

        %
        % Prior distributions - assumed to be Normal
        %
        P.pkdv.mean = zeros(tableSize,1);
        P.pkdv.std  = 5*ones(tableSize,1);
        % P.pkdv.mean(P.thetaColumnsRationalityXIndiv) = -2;
        % P.pkdv.std(P.thetaColumnsRationalityXIndiv) = 1;
        P.pkdv.columns = [1:tableSize]';

        %
        % Name the parameters
        %
        P.modelParameterNames = {...
                        'beta_0_p3',...
                        'beta_0_att4cert',...
                        'beta_1_c',...
                        'beta_2_price',...
                        'beta_2_posterior',...
                        'beta_3_quality',...
                        'explogsigma',...
                        'beta_4_rationality_hiconscien',...
                        'beta_4_rationality_impuls',...
                        'beta_4_rationality_c',...
                        'beta_5_clarity_himarketexper',...
                        'beta_5_clarity_hiproductknow',...
                        'beta_5_clarity_age40over',...
                        'beta_5_clarity_gender',...
                        'beta_5_clarity_hifinlit',...
                        'beta_5_clarity_hinum',...
                        'beta_5_superConsolidation',...
                        'beta_5_diversification',...
                        'beta_5_fees',...
                        'beta_5_debtConsolidation'...
        };

        if isdir(outpath)
            fprintf('\n%s is the output storage directory - existing files in that directory will be overwritten.\n',outpath);
        else
            mkdir(outpath);
            fprintf('\n%s is the output storage directory and has been created as a new directory.\n',outpath);
        end

        diary([outpath '/summary.txt']);
        diary on;

        % Execute SABL
        SABL;


        %  Setup thetahat (optimal theta)
        thetahat = u_allocate([1 tableSize],'default','zeros');
        stdhat = u_allocate([1 tableSize],'default','zeros');
        meanhat = u_allocate([1 tableSize],'default','zeros');
        pc2_5 = u_allocate([1 tableSize],'default','zeros');
        pc97_5 = u_allocate([1 tableSize],'default','zeros');

        for ii=1:tableSize
            thetahat(ii) = u_mode(Cpar.theta(:,ii),100);
            stdhat(ii) = std(Cpar.theta(:,ii));
            meanhat(ii) = mean(Cpar.theta(:,ii));
            pc2_5(ii) = prctile(Cpar.theta(:,ii),2.5);
            pc97_5(ii) = prctile(Cpar.theta(:,ii),97.5);
        end



        % log sigma must first be transformed back to sigma for display
        thhat2 = thetahat;
        thhat2(P.thetaColumnsSigma) = exp(u_mode(Cpar.theta(:,P.thetaColumnsSigma),100));
        stdhat(P.thetaColumnsSigma) = std(exp(Cpar.theta(:,P.thetaColumnsSigma)));
        meanhat(P.thetaColumnsSigma) = exp(mean(Cpar.theta(:,P.thetaColumnsSigma)));
        pc2_5(P.thetaColumnsSigma) = exp(prctile(Cpar.theta(:,P.thetaColumnsSigma),2.5));
        pc97_5(P.thetaColumnsSigma) = exp(prctile(Cpar.theta(:,P.thetaColumnsSigma),97.5));

        thtable = table(thhat2',meanhat',stdhat',pc2_5',pc97_5',P.pkdv.mean(1:tableSize),P.pkdv.std(1:tableSize),'VariableNames',{'Mode','Mean','StdDev','TwoPointFivePercentile','NinetySevenPointFivePercentile','PriorMean','PriorStdDev'},'RowNames', P.modelParameterNames);

        % Temporary fixed s - remove the entry from thtable
        thtable(3,:) = [];

        % Save Cpar.theta to a .csv
        csvName = sprintf('posteriorDistributions.csv');
        tableForCsv = array2table(gather(Cpar.theta(:,1:tableSize)),'VariableNames',P.modelParameterNames);
        writetable(tableForCsv,[outpath '/' csvName]);
        fprintf('\n\nCSV file written with posterior simulated parameter values: %s\n', csvName);

SABL_results/Specification3/beta_0 = p3,att4cert/beta_1 = c/beta_2 = posterior,wtp/beta_3 = quality/beta_4 = c,hiimpuls,hiconscien/beta_5 = topics,himarketexper,hiprodknow,age40over,gender,hifinlit,hinum/price zero-mean adjusted, all individual characteristics +1-1 coded, multiplicative sigma, fixed s = 0.75 is the output storage directory - existing files in that directory will be overwritten.

SABL executing using GPU with 8 workers

C phase anneal_Bayes algorithm
Effective sample size criterion (C.Cstop.ress) = 0.500

C phase Cstop_unconditional algorithm

S phase residual resampling

M phase MGRW_simple algorithm
   Initial step size (C.Mphase.step_initial) = 0.500
     Minimum step size (C.Mphase.step_lower) = 0.100
     Maximum step size (C.Mphase.step_upper) = 2.000
   Step size increment (C.Mphase.step_upper) = 0.100
Acceptance rate target (C.Mphase.acceptgoal) = 0.250

M phase Mstop_rne stopping algorithm
                  RNE criterion (C.Mstop.rne) = 0.400
   Last cycle RNE criterion (C.Mstop.rne_end) = 0.900
               Bound on steps (C.Mstop.steps) = 100
Last cycle bound on steps (C.Mstop.steps_end) = 300

The helper script (compile_cuda.m) was not found...skipping compilation of CUDA/mex kernel...
Lab 1: 
  Cycle    1 Cphase: Likelihood function exponent 9.2967e-05, RESS 0.5000
  Cycle    1 Sphase: 1735 particles out of 3072 unique (0.5648)
  Cycle    1 Mphase:   1 iterations, mean RNE =  0.5227
  Cycle    2 Cphase: Likelihood function exponent 3.0458e-04, RESS 0.5000
  Cycle    2 Sphase: 1010 particles out of 3072 unique (0.3288)
  Cycle    2 Mphase:  17 iterations, mean RNE =  0.4015
  Cycle    3 Cphase: Likelihood function exponent 7.8409e-04, RESS 0.5000
  Cycle    3 Sphase: 1740 particles out of 3072 unique (0.5664)
  Cycle    3 Mphase:  13 iterations, mean RNE =  0.4059
  Cycle    4 Cphase: Likelihood function exponent 1.8274e-03, RESS 0.5000
  Cycle    4 Sphase: 1742 particles out of 3072 unique (0.5671)
  Cycle    4 Mphase:   8 iterations, mean RNE =  0.4047
  Cycle    5 Cphase: Likelihood function exponent 3.7945e-03, RESS 0.5000
  Cycle    5 Sphase: 1765 particles out of 3072 unique (0.5745)
  Cycle    5 Mphase:  12 iterations, mean RNE =  0.4064
  Cycle    6 Cphase: Likelihood function exponent 6.8640e-03, RESS 0.5000
  Cycle    6 Sphase: 1821 particles out of 3072 unique (0.5928)
  Cycle    6 Mphase:  16 iterations, mean RNE =  0.4160
  Cycle    7 Cphase: Likelihood function exponent 1.0753e-02, RESS 0.5000
  Cycle    7 Sphase: 1865 particles out of 3072 unique (0.6071)
  Cycle    7 Mphase:  18 iterations, mean RNE =  0.4098
  Cycle    8 Cphase: Likelihood function exponent 1.5499e-02, RESS 0.5000
  Cycle    8 Sphase: 1902 particles out of 3072 unique (0.6191)
  Cycle    8 Mphase:  26 iterations, mean RNE =  0.4045
  Cycle    9 Cphase: Likelihood function exponent 2.1362e-02, RESS 0.5000
  Cycle    9 Sphase: 1874 particles out of 3072 unique (0.6100)
  Cycle    9 Mphase:  15 iterations, mean RNE =  0.4048
  Cycle   10 Cphase: Likelihood function exponent 2.9389e-02, RESS 0.5000
  Cycle   10 Sphase: 1800 particles out of 3072 unique (0.5859)
  Cycle   10 Mphase:  34 iterations, mean RNE =  0.4063
  Cycle   11 Cphase: Likelihood function exponent 4.0795e-02, RESS 0.5000
  Cycle   11 Sphase: 1840 particles out of 3072 unique (0.5990)
  Cycle   11 Mphase:  41 iterations, mean RNE =  0.4006
  Cycle   12 Cphase: Likelihood function exponent 5.6437e-02, RESS 0.5000
  Cycle   12 Sphase: 1884 particles out of 3072 unique (0.6133)
  Cycle   12 Mphase:  65 iterations, mean RNE =  0.4096
  Cycle   13 Cphase: Likelihood function exponent 7.5681e-02, RESS 0.5000
  Cycle   13 Sphase: 1884 particles out of 3072 unique (0.6133)
  Cycle   13 Mphase:  94 iterations, mean RNE =  0.4036
  Cycle   14 Cphase: Likelihood function exponent 9.7348e-02, RESS 0.5000
  Cycle   14 Sphase: 1887 particles out of 3072 unique (0.6143)
  Cycle   14 Mphase:  89 iterations, mean RNE =  0.4050
  Cycle   15 Cphase: Likelihood function exponent 1.2142e-01, RESS 0.5000
  Cycle   15 Sphase: 1890 particles out of 3072 unique (0.6152)
  Cycle   15 Mphase: 100 iterations, mean RNE =  0.3376
  Cycle   16 Cphase: Likelihood function exponent 1.4717e-01, RESS 0.5000
  Cycle   16 Sphase: 1905 particles out of 3072 unique (0.6201)
  Cycle   16 Mphase:  94 iterations, mean RNE =  0.4011
  Cycle   17 Cphase: Likelihood function exponent 1.7638e-01, RESS 0.5000
  Cycle   17 Sphase: 1855 particles out of 3072 unique (0.6038)
  Cycle   17 Mphase:  48 iterations, mean RNE =  0.4078
  Cycle   18 Cphase: Likelihood function exponent 2.1533e-01, RESS 0.5000
  Cycle   18 Sphase: 1816 particles out of 3072 unique (0.5911)
  Cycle   18 Mphase:  42 iterations, mean RNE =  0.4038
  Cycle   19 Cphase: Likelihood function exponent 2.6405e-01, RESS 0.5000
  Cycle   19 Sphase: 1862 particles out of 3072 unique (0.6061)
  Cycle   19 Mphase:  17 iterations, mean RNE =  0.4054
  Cycle   20 Cphase: Likelihood function exponent 3.2273e-01, RESS 0.5000
  Cycle   20 Sphase: 1808 particles out of 3072 unique (0.5885)
  Cycle   20 Mphase:  52 iterations, mean RNE =  0.4050
  Cycle   21 Cphase: Likelihood function exponent 3.9844e-01, RESS 0.5000
  Cycle   21 Sphase: 1857 particles out of 3072 unique (0.6045)
  Cycle   21 Mphase:  38 iterations, mean RNE =  0.4077
  Cycle   22 Cphase: Likelihood function exponent 4.9825e-01, RESS 0.5000
  Cycle   22 Sphase: 1865 particles out of 3072 unique (0.6071)
  Cycle   22 Mphase:   6 iterations, mean RNE =  0.4045
  Cycle   23 Cphase: Likelihood function exponent 6.2231e-01, RESS 0.5000
  Cycle   23 Sphase: 1597 particles out of 3072 unique (0.5199)
  Cycle   23 Mphase:  42 iterations, mean RNE =  0.4022
  Cycle   24 Cphase: Likelihood function exponent 7.7199e-01, RESS 0.5000
  Cycle   24 Sphase: 1897 particles out of 3072 unique (0.6175)
  Cycle   24 Mphase:  54 iterations, mean RNE =  0.4062
  Cycle   25 Cphase: Likelihood function exponent 9.7865e-01, RESS 0.5000
  Cycle   25 Sphase: 1845 particles out of 3072 unique (0.6006)
  Cycle   25 Mphase:  37 iterations, mean RNE =  0.4008
  Cycle   26 Cphase: Likelihood function exponent 1.0000e+00, RESS 0.9929
  Cycle   26 Sphase: 2665 particles out of 3072 unique (0.8675)
  Cycle   26 Mphase: 131 iterations, mean RNE =  0.9009
  
  Log marginal likelihood
               Approximation    Numerical standard error
     w-bar:       -6045.1668                      0.4593
   w-tilde:       -6046.0467                      0.4593

 Elapsed clock time    1713.84 seconds
           CPU time      26.52 seconds
              Ratio       0.02
 (Interpretation of CPU time is installation specific.)

Run is complete.


CSV file written with posterior simulated parameter values: posteriorDistributions.csv

Summary

        fprintf('\n     Updating scheme: Specification 3: unobserved 16 clarity classes, unobserved 2 rationality classes\n' );
      % fprintf(  '     sigma = %.4f\n', P.fixedSigma);
        fprintf(  '     s = %.2f\n',P.fixedS);

        fprintf('\n     Summary of parameter estimates:\n\n');
        disp(thtable);
        fprintf('    Log ML: %.2f\n',C.logml1);

        pmpn = strrep(strrep(strrep(P.modelParameterNames,'_',''),'beta0','\beta_0'),'beta4','\beta_4')';
        pmpn = strrep(pmpn,'beta1','\beta_1');
        pmpn = strrep(pmpn,'beta2','\beta_2');
        pmpn = strrep(pmpn,'beta30','\beta_3^0');
        pmpn = strrep(pmpn,'beta31','\beta_3^1');
        pmpn = strrep(pmpn,'beta32','\beta_3^2');
        pmpn = strrep(pmpn,'beta33','\beta_3^3');
        pmpn = strrep(pmpn,'beta34','\beta_3^4');
        pmpn = strrep(pmpn,'beta35','\beta_3^5');
        pmpn = strrep(pmpn,'beta4','\beta_4');
        pmpn = strrep(pmpn,'beta5','\beta_5');
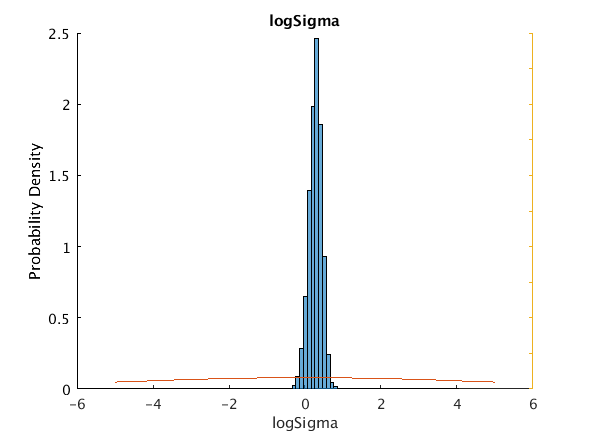
        pmpn{P.thetaColumnsSigma} = 'logSigma';
        for ii = 1:tableSize
            if ii ~= 3  % temporarily remove beta1_s
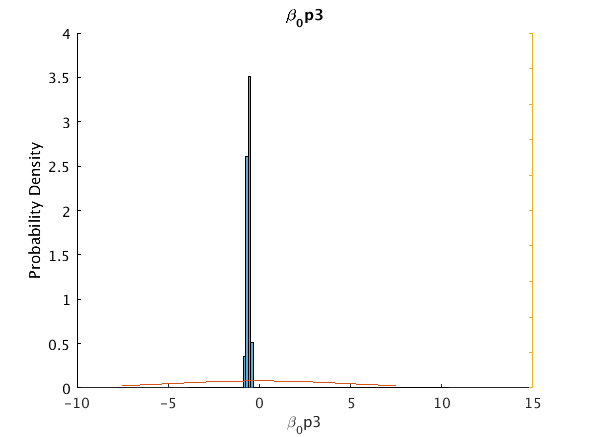
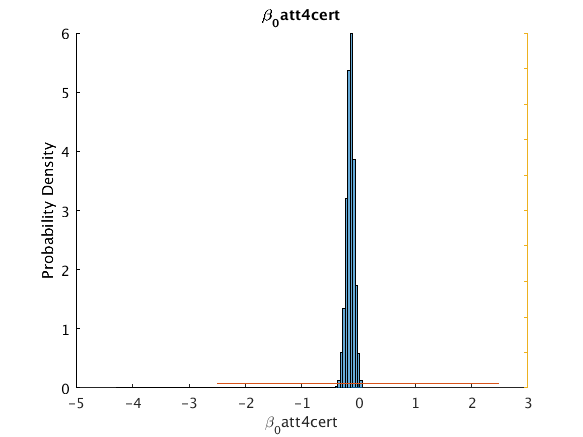
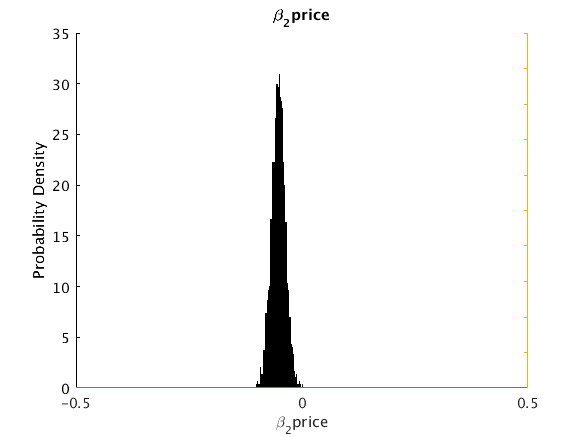
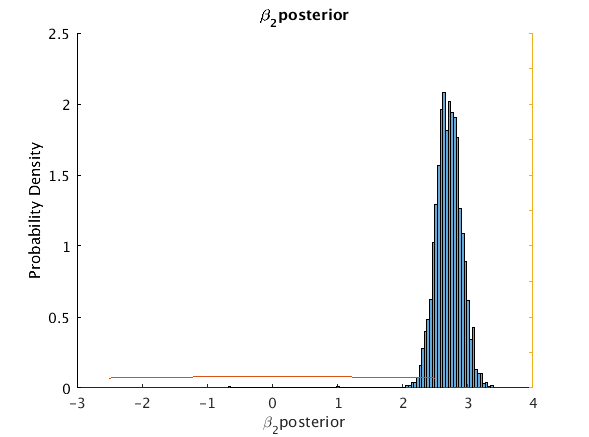
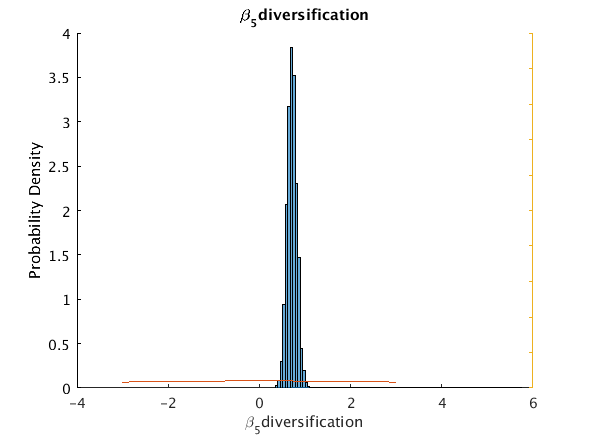
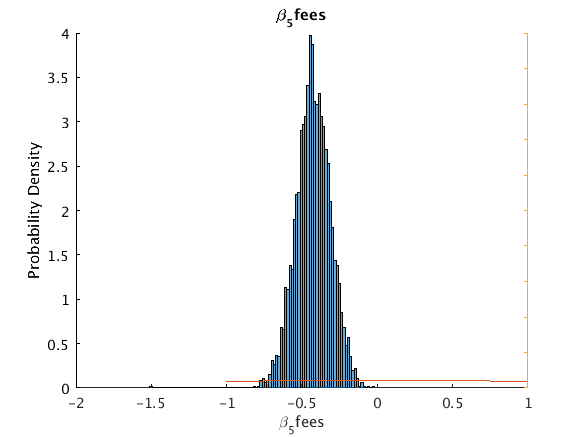
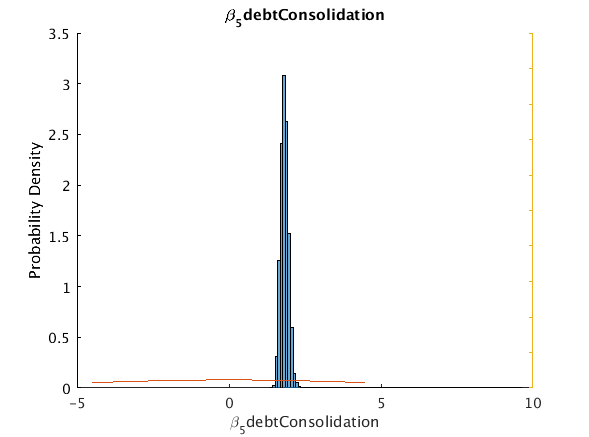
                u_hisfig(Cpar.theta(:,ii),100,pmpn{ii},pmpn{ii},outpath);
            end
        end

     Updating scheme: Specification 3: unobserved 16 clarity classes, unobserved 2 rationality classes
     s = 0.75

     Summary of parameter estimates:

                                       Mode         Mean        StdDev     TwoPointFivePercentile    NinetySevenPointFivePercentile    PriorMean    PriorStdDev
                                     _________    _________    ________    ______________________    ______________________________    _________    ___________

    beta_0_p3                          -0.5395     -0.59388     0.22645     -0.79602                  -0.425267                        0            5          
    beta_0_att4cert                   -0.12575     -0.14591     0.10868     -0.28612                 -0.0119029                        0            5          
    beta_2_price                     -0.049403    -0.051817    0.014505    -0.079837                 -0.0232419                        0            5          
    beta_2_posterior                     2.637       2.7056     0.20324       2.3254                    3.08265                        0            5          
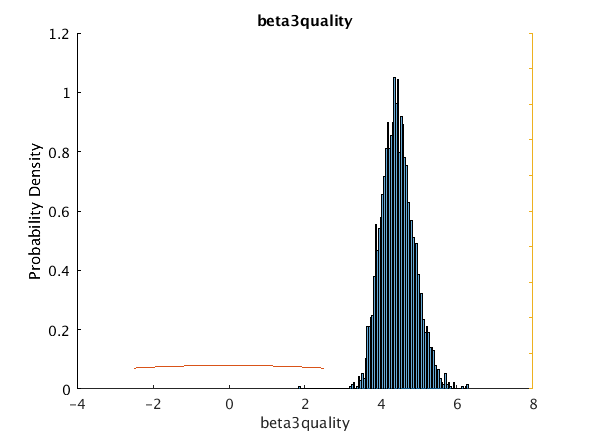
    beta_3_quality                      4.3599       4.4423      0.4351       3.6762                    5.36379                        0            5          
    explogsigma                         1.3634       1.3098      1.0443      0.92368                    1.77977                        0            5          
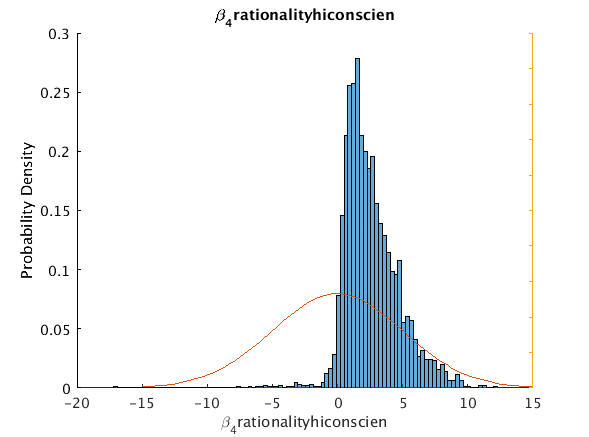
    beta_4_rationality_hiconscien       1.5325       2.6011      2.1103     -0.17568                    7.64861                        0            5          
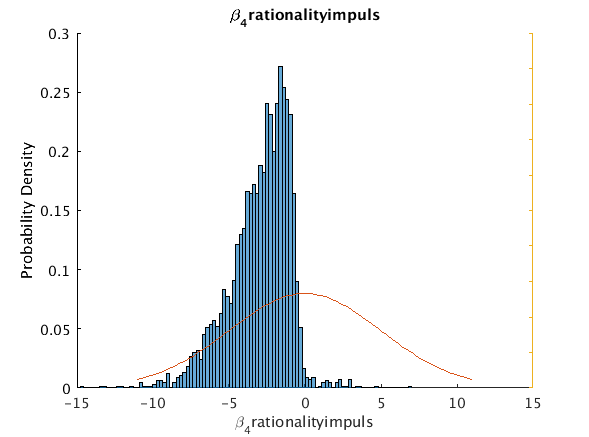
    beta_4_rationality_impuls           -1.611      -2.9677      1.9981      -7.4823                  -0.330335                        0            5          
    beta_4_rationality_c                4.9065        6.076      2.6072       1.9655                    12.0413                        0            5          
    beta_5_clarity_himarketexper       0.14851      0.16256     0.05239     0.066939                   0.269276                        0            5          
    beta_5_clarity_hiproductknow       0.28955      0.29212    0.072927      0.19253                   0.394111                        0            5          
    beta_5_clarity_age40over           0.54212      0.51933    0.056123      0.41285                   0.630356                        0            5          
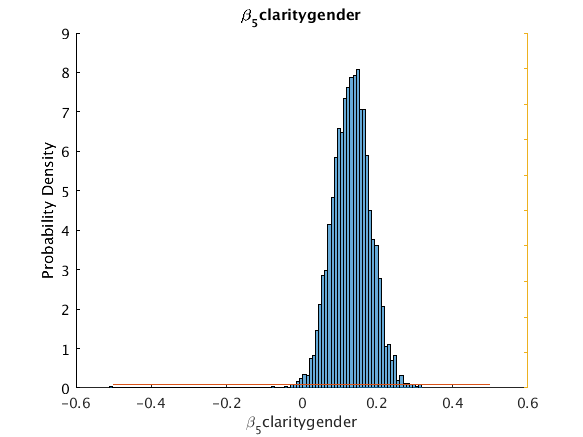
    beta_5_clarity_gender              0.14785      0.13185    0.051296     0.036679                    0.23067                        0            5          
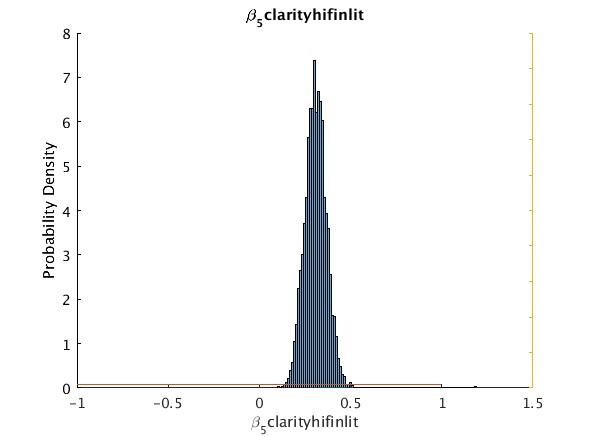
    beta_5_clarity_hifinlit            0.30165      0.30894    0.060537       0.1974                   0.423668                        0            5          
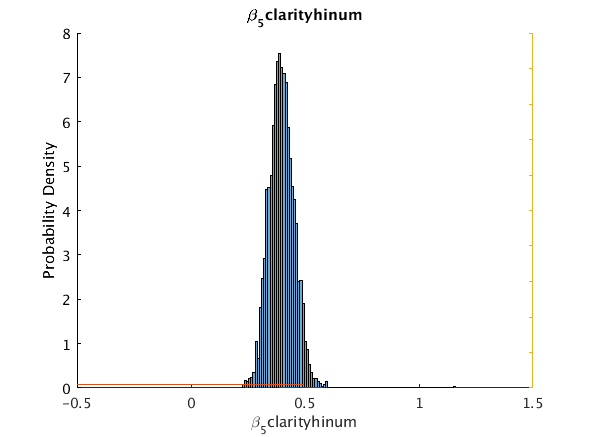
    beta_5_clarity_hinum               0.38898      0.39795    0.056098       0.2979                   0.507436                        0            5          
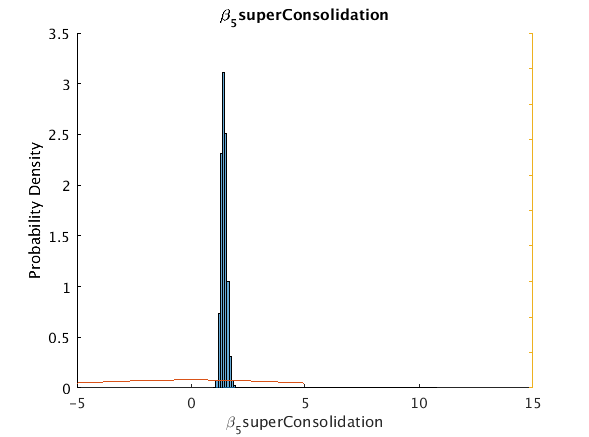
    beta_5_superConsolidation            1.431       1.4526     0.20839       1.2288                    1.70133                        0            5          
    beta_5_diversification              0.7023      0.71541     0.13734      0.51819                   0.918905                        0            5          
    beta_5_fees                       -0.44465     -0.42546     0.11541     -0.65478                   -0.20005                        0            5          
    beta_5_debtConsolidation             1.816       1.8347     0.18887       1.6015                    2.08836                        0            5          

    Log ML: -6045.17

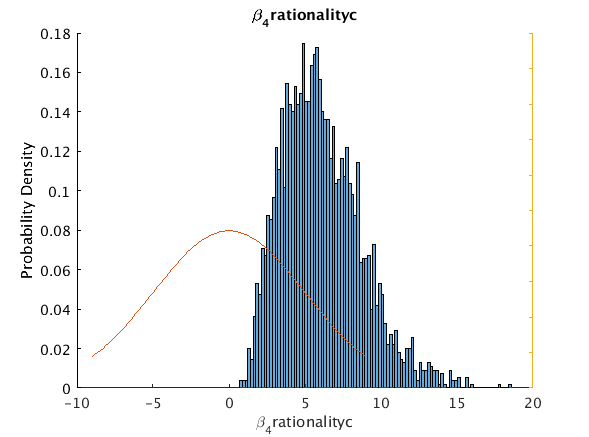
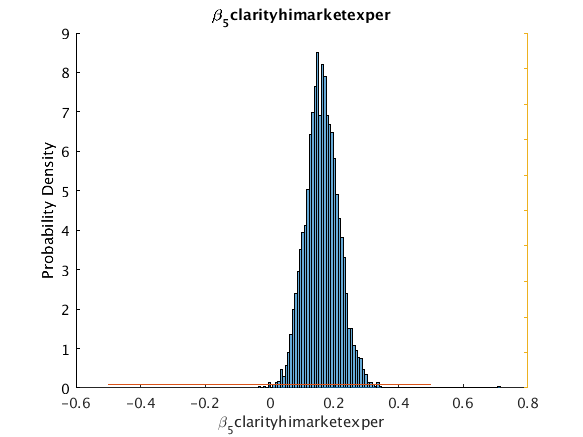
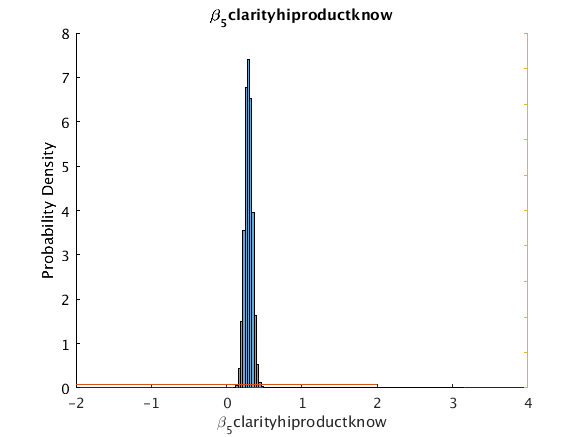
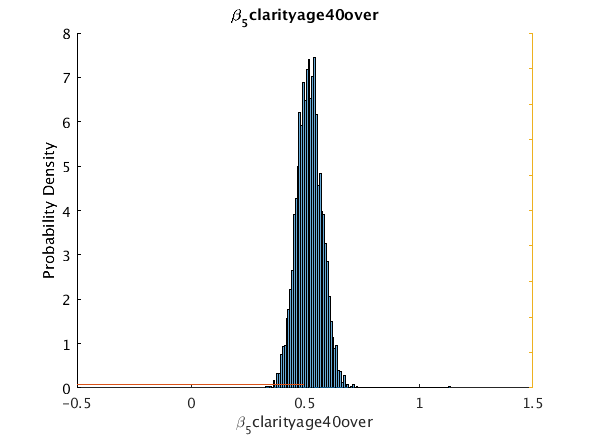
Move post-processing to CPU to avoid memory limitations

        Cpar.theta=gather(Cpar.theta);
        Cpar.logp=gather(Cpar.logp);
        Cpar.logpinc=gather(Cpar.logpinc);
        Cpar.logpw=gather(Cpar.logw);
        M.data=gather(M.data);
        P.d_Quality = gather(P.d_Quality);
        P.d_Quality_R = gather(P.d_Quality_R);
        P.d_Clarity = gather(P.d_Clarity);
        P.updateRational = gather(P.updateRational);
        P.updateRational_R = gather(P.updateRational_R);

        thetahat = gather(thetahat);
        stdhat = gather(stdhat);
        meanhat = gather(meanhat);
        pc2_5 = gather(pc2_5);
        pc97_5 = gather(pc97_5);
        gpuDevice(1);

        E.gpu = false;

        % Class memberships

        [~,~,tCl_ensm,tRa_ensm] = m_message(Cpar.theta,1);
        topic_l=squeeze(P.d_ClarityT);
        prop_cl_ensm = squeeze(sum(exp(tCl_ensm),1)./size(tCl_ensm,1));
        fprintf('\n*** Clarity class membership statistics ***\n\n');
        clmode = [ u_mode(100*prop_cl_ensm(:,1),100) u_mode(100*prop_cl_ensm(:,2),100) u_mode(100*prop_cl_ensm(:,3),100) u_mode(100*prop_cl_ensm(:,4),100)...
          u_mode(100*prop_cl_ensm(:,5),100) u_mode(100*prop_cl_ensm(:,6),100) u_mode(100*prop_cl_ensm(:,7),100) u_mode(100*prop_cl_ensm(:,8),100)...
          u_mode(100*prop_cl_ensm(:,9),100) u_mode(100*prop_cl_ensm(:,10),100) u_mode(100*prop_cl_ensm(:,11),100) u_mode(100*prop_cl_ensm(:,12),100)...
          u_mode(100*prop_cl_ensm(:,13),100) u_mode(100*prop_cl_ensm(:,14),100) u_mode(100*prop_cl_ensm(:,15),100) u_mode(100*prop_cl_ensm(:,16),100)];

        tableCmem_ensm = table(topic_l(:,1),topic_l(:,2),topic_l(:,3),topic_l(:,4), mean(100*prop_cl_ensm,1)', clmode', std(100*prop_cl_ensm,0,1)','VariableNames',{'SuperConsolidation','Diversification','Fees','DebtConsolidation','Mean','Mode','StdDev'});
        disp(tableCmem_ensm);
        disp(' ');

        if ~(P.forceRational || P.forceFryer)
            fprintf('\n*** Rationality class membership statistics ***\n\n');
            prop_ra_ensm = squeeze(sum(exp(tRa_ensm),1)./size(tRa_ensm,1));

            tableRmem_ensm = table(mean(100*prop_ra_ensm,1)',[u_mode(100*prop_ra_ensm(:,1),100) u_mode(100*prop_ra_ensm(:,2),100)]',std(100*prop_ra_ensm,0,1)','VariableNames',{'Mean','Mode','StdDev'},'RowNames',{'Rational','Fryer'});
            disp(tableRmem_ensm);
            disp(' ');
        end

*** Clarity class membership statistics ***

    SuperConsolidation    Diversification    Fees    DebtConsolidation     Mean       Mode      StdDev 
    __________________    _______________    ____    _________________    _______    ______    ________

    1                     1                  1       1                     20.526    20.333       1.538
    1                     1                  1       0                     2.2652    2.2171     0.27365
    1                     1                  0       1                     21.543    21.225      1.3283
    1                     1                  0       0                     4.2955    4.1295     0.44031
    1                     0                  1       1                     6.9111    7.0744     0.65142
    1                     0                  1       0                     1.3801    1.3525     0.18236
    1                     0                  0       1                     13.111    13.114     0.87504
    1                     0                  0       0                     4.5558    4.5689     0.43822
    0                     1                  1       1                     3.3193    3.3135     0.38788
    0                     1                  1       0                     0.6639    0.6519     0.10525
    0                     1                  0       1                     6.2902    6.2113     0.57323
    0                     1                  0       0                     2.1868    2.2094     0.25091
    0                     0                  1       1                     2.0225    1.9485        0.26
    0                     0                  1       0                    0.70222    0.7074    0.096418
    0                     0                  0       1                     6.6734    6.7568     0.59056
    0                     0                  0       0                     3.5544    3.4379     0.46251

 

*** Rationality class membership statistics ***

                 Mean     Mode     StdDev
                ______    _____    ______

    Rational    83.517    83.83    5.0335
    Fryer       16.483    16.17    5.0335

Prediction - in sample

        u_predict(P.dataRowsInEstimation,'In Sample',spec2,thetahat);


*** Prediction - In Sample ***

For 1903 randomly chosen rows:

                                    Model_Probability    Observed_RelativeFrequency
                                    _________________    __________________________

    WTP Advisor L                   0.48657              0.39779                   
    WTP Advisor R                   0.48743              0.39044                   
    Advisor R chosen in Choice 1    0.49753              0.51971                   
    Advisor R chosen in Choice 2    0.50499               0.5381                   
    Advisor R chosen in Choice 3    0.50037              0.53232                   
    Advisor R chosen in Choice 4    0.49988              0.52076                   

When Advisor R was observed as chosen, the model predicted probability of choosing Advisor R, averaged over 4 choicesets, was: 0.69
When Advisor R was observed as not chosen, the model predicted probability of choosing Advisor R, averaged over 4 choicesets, was: 0.29
When chosen to be paid, the model predicted probability of being paid, averaged over Advisor L and Advisor R, was: 0.51
When not chosen to be paid, the model predicted probability of being paid, averaged over Advisor L and Advisor R, was: 0.47

Prediction - out of sample

        u_predict(P.dataRowsHeldOut,'Held Out Sample',spec2,thetahat)

        diary off;


*** Prediction - Held Out Sample ***

For 100 randomly chosen rows:

                                    Model_Probability    Observed_RelativeFrequency
                                    _________________    __________________________

    WTP Advisor L                   0.48583              0.38                      
    WTP Advisor R                   0.48057              0.41                      
    Advisor R chosen in Choice 1    0.52162              0.55                      
    Advisor R chosen in Choice 2    0.47018              0.47                      
    Advisor R chosen in Choice 3    0.50913              0.55                      
    Advisor R chosen in Choice 4    0.49556              0.56                      

When Advisor R was observed as chosen, the model predicted probability of choosing Advisor R, averaged over 4 choicesets, was: 0.70
When Advisor R was observed as not chosen, the model predicted probability of choosing Advisor R, averaged over 4 choicesets, was: 0.28
When chosen to be paid, the model predicted probability of being paid, averaged over Advisor L and Advisor R, was: 0.50
When not chosen to be paid, the model predicted probability of being paid, averaged over Advisor L and Advisor R, was: 0.47

end

Contents

SABL

Summary

Move post-processing to CPU to avoid memory limitations

Prediction - in sample

Prediction - out of sample